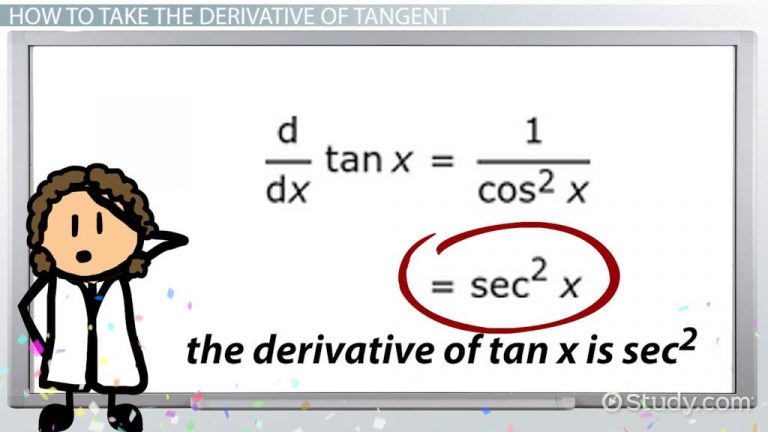So if you are currently in high school, you would know that trigonometry and calculus are probably the two most important aspects of math. So, you can find almost nothing where you do not need either one of them or both. Moreover, it is not just for solving sums in math that you need them. You will also find their wide applications in economics, physics, chemistry, statistics- nearly everything, so to say. The role they play behind the formation of curves is one of the prime reasons why this happens. Moreover, as you engage in any scientific higher study, you realize how important curves are, like a tan derivative. So, you need trigonometry as well as calculus to help you calculate and understand them. Now, differentiation means you break a quantity into infinitesimally small quantities. Integration is when you up extremely small quantities to form one single and larger entity.

However, we will see in the later sections why this understanding of differentiation is crucial in understanding a tan derivative.

So, we are already aware that the primary trigonometric functions are sin, cos, tan, cosec, sec, and cot. Therefore, tan is the short form of the tangent. However, amongst these functions, when you have to differentiate, the outcome or the resultant derivative is another trigonometric function. This makes sense because a tan derivative of x cannot be x^3, let us say. Therefore, when it comes to using calculus to trigonometric values, there are some rules that you must keep in mind. However, in this article, we will concentrate only on a tan derivative and its rules, formula, definition, ways to find it, and so on.

Tan derivative function

So, we all know that the tangent is the ratio of the perpendicular to the base of the triangle. Moreover, we also are aware that cosine is the ratio of the base to the hypotenuse of the triangle. Hence, the secant becomes the ratio of the hypotenuse to the base of the triangle because it is the reciprocal of cosine. Therefore, now, the tan derivative is a function of the secant or sec of that particular angle. Let us see how.

So, let us say the angle with respect to which we will calculate the trigonometric functions is x.

Hence, we have got the functions sin x, cos x, and tan x. Now, from our trigonometry knowledge, we should know that tan x = sin x/ cos x. How does this happen? So, this is because sin x is the ratio of the perpendicular to the hypotenuse of the triangle while cos x is that of the base to the hypotenuse. So, when you divide them, you cancel the hypotenuse. Additionally, we can also derive that sec x = 1/ cos^2x.

So, using this we will be finding the tan derivative in the next section.

But, before that let us see the quotient rule once. As per the quotient rule, you differentiate the numerator at first and then multiply it with the denominator. So, after this, you have to differentiate the denominator and again multiply it with the numerator. Finally, subtract it from the first term. After this, you have to divide the entire expression by the square of the denominator.

We know that the derivative of a trigonometric function is generally another trigonometric function. So, for the tangent, or a tan derivative, the resulting function is the square of the secant or sec^2 the variable.

Tan derivative proof

So, we have tan x.

However, we can write this sin x/ cos x. Now, let us differentiate this and find out the tan derivative using the quotient rule. Moreover, as per the laws of differentiation, d/ dx (sin x) = cos x and d/ dx(cos x) = – sin x. So,

d/ dx (tan x) = d/ dx ( sin x/ cos x)

Or, d/ dx (tan x) = (cos x * (d/ dx (sin x)) – sin x * (d/ dx (cos x))) / cos^2 x, following the product rule.

So, d/ dx (tan x) = (cos x * cos x – ( sin x * (- sin x)) / cos^2 x.

Therefore, d/ dx (tan x) = (cos^2 x + sin^2 x) / cos^2 x.

However, we also know that cos^2 x + sin^2 x = 1, as per the laws of trigonometry.

Hence, d/ dx (tan x) = 1/ cos^2 x. (We already know that the reciprocal of cos is sec). So, 1/ cos^2 x will be sec^2 x. Therefore, this is how we find the solution to a tan derivative.

The above image shows how you can derive the proof using the first principle with limits. However, it makes the process more complex than is necessary. However, here too, what you end up getting is 1/ ( cos x * cos x) which 1/ cos^2 x. Therefore, the end result is again sec^2 x. So no matter what method you apply, as long as you are correct and your steps are mathematically flawless, the tan derivative is square of sec.

Tan derivative differentiation

So, we already know what differentiation is. Moreover, we have just now seen the proof of a tan derivative using differentiation. However, when we talk about differentiation, there is also another aspect. So, differentiation also helps to find out the rate of change in a function. So, that works for a tan derivative too. Tangents generally form the slope of a graph which means it represents the rate of change. Differentiation does the same work. So they essentially mean the same.

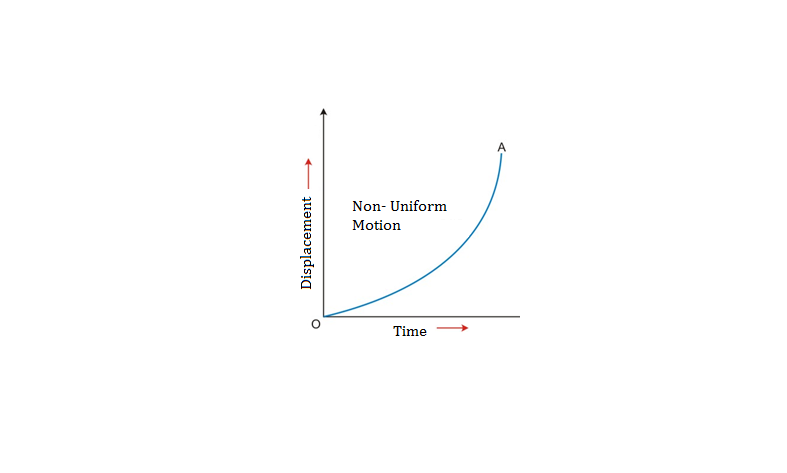
Example in a graph

Let us understand this with an example. So, say you are plotting a graph. On the x-axis, you have plotted the displacement a car covers and on the y-axis the corresponding time in which it covers that much displacement. Now, let us say the acceleration does not remain constant. So, you get a curved line. Now, the slope of the graph gives you the rate of change at any point on the curve. Therefore, to do this you need to draw a tangent at any point on the curve and find it. However, you will find the same result if you differentiate the function of the line at that point.

Tan derivative formula

So, we have already seen the formula of the tan derivative from the proof. Therefore, if x is the variable or the angle whose tangent we are considering, d/ dx (tan x ) = sec^2 x. However, this is different if there is an inverse function that we will see later on.

Moreover, you might not always need the derivation of a tan derivative but remembering the formula is essential for any future calculations that you might need to do.

Tan derivative definition

So, you cannot really define a derivative because it is practically a function. However, in plain and simple terms, it is the rate at which the tangent of an angle changes at any particular instant. You can derive it via the quotient rule as we already saw or via limits using the first principle. However, the latter is a way more complex process.

Tan derivative rules

There are no special rules to deal with or find out a tan derivative. So, all that you need to keep in mind are some trigonometry and derivative rules that we have already seen. Therefore, what you need to remember are the product rule of derivatives and the primary laws of trigonometry that helps you conduct the differentiation. For a tan derivative, in particular, there is no other rule. However, we can quickly check the inverse rule to find out a tan inverse derivative.

Tan inverse derivative

Now, we already know the derivatives of a tangent. We have also seen in detail the proof and rules for a tan derivative. So, from here, the next best thing to do is probably to see the inverse of a tan derivative.

Therefore, in trigonometry, we get plenty of inverse functions. For example, the inverse of the tangent is written as tan^(-1) x. So, it is important to note that the derivatives of the tangent inverse are not the same as the normal derivatives of the tangent. So, it is 1/ (1 + x^2)

Therefore, let us see how.

So, we have the function f(x) = tan^(-1)x

Hence, let y = tan^(-1)x

So, tan y = x (This is because tan(tan^(-1)x) = x)

⇒ x = tan y → (1)

Now, we will have to differentiate both sides of x = tan y w.r.t. x

(dx/dx) = d(tan y)/dx

So, 1 = [d(tan y)/dx] × [dy/dy] [Multiplying and dividing by ‘dy’]

Or, 1 = [d(tan y)/dy] × [dy/dx]

So, 1 = [sec^2y] dy/dx (we already know that d(tan x)/dx = sec^2x)

Or, 1 = [1 + tan^2y] dy/dx [Using trigonometric laws, sec^2y = 1 + tan^2y]

dy/dx = [1] / [1 + tan^2y]

Substituting tan y = x (from (1)) into dy/dx = [1] / [1 + tan^2y], we have

dy/dx = 1 / (1 + x^2)

⇒ d(tan^(-1)x)/dx = 1 / (1 + x^2)

Hence, we have derived the derivative of tan inverse x using implicit differentiation.

Tan derivative of y

So, this might mean two things. While differentiating, we generally assign a function to be y. So, consider the function is tan x ( let us say x is the angle in consideration). Hence, to find the tan derivative, you simply differentiate it with respect to x, that is dy/ dx. This is what we have been doing so far. However, it might also mean that y is another function whose tangent we have to find and then differentiate. Let us say y = x^2 + 1. Therefore, in that case, the tan derivative of y will become d/dx ( tan y * dy/dx) because here y is no more tan x. So, you differentiate y which gives you 2x after you differentiate tan. Therefore, you need the chain rule of derivatives to complete the process and get the final answer.

Tan derivative calculator

There are various online calculators out there with which you can find a tan derivative. So, in some cases, the calculator can only find a tan derivative. However, in most cases, you get a general online derivative calculator where you can very well find a tan derivative. Now, using a tan derivative calculator helps you in many ways. To begin with, if the sum is complex and you cannot solve it, it is always there for you. Moreover, if you solve a sum and see the solution, you actually have a better understanding because math is a subject that is based on application. Finally, it might also happen that you are making a mistake somewhere in your calculator because we are all human beings. So, in those cases, it is always you run the sum with the calculator and verify.

This is particularly important when you are doing a complex sum and a little mistake can go a long way.

However, the problem is not all of these online calculators are free. In fact, for most of them, you need to pay for some kind of subscription. On the other hand, in most of the free ones, you cannot feed in your own answer and check where you went wrong or if there is a glitch in the calculator. So, there are both pros and cons but there are a lot of options out there for you to suit yourself.

Moreover, the basic steps in all calculators more or less remain the same. Let us see how.

Step 1:

So, the first step is to find a calculator that will suit you the best online. Now, once you find it out, irrespective of the calculator, you will find a box that looks like a search engine. So, type in your data there- d/dx (tan x). “X” can be any variable or expression as per your problem at hand. Let us say, you take d/ dx (tan x^3)

Step 2:

No matter what calculator you use, you will find a button beside or under the box that looks like a search engine where you enter the data. So, it might say things like “run” or “go”, etc. Basically, you have to click it for the sum to run and for the calculator to find the tan derivative. It might take a few seconds before you get the answer.

Step 3:

So, finally, you can get the answer. For the example we are using, it will be sec^2 x^3 * 3x^2. So, this is because we have applied the chain rule. Therefore, we have differentiated x^3 as well. If you are not using a paid one, you get only the answer. However, if you are using a paid calculator, you can see all the steps in the solution. Moreover, in some calculators, you can also check if your answer is right in case you are dissatisfied with the calculator’s answer. There will be another box that looks like a search engine where you enter this data.

Tan derivative FAQs

What is the derivative of tan?

Ans. So, by differentiation, the derivative of tangent or tan derivative is secant squared or sec^2 the angle. To know more, scroll up and check the “tan derivative function” section and you will have a better understanding.

Is tan x continuous?

Ans. So, yes, the function tan(x) is continuous everywhere but not at the points kπ. Hence, similarly, the function cot(x) is continuous everywhere but not at points π/2 + kπ.

Is tan differentiable?

Ans. Yes, tan is a function that is both continuous and differentiable. Hence, we can have a tan derivative as the article shows. However, we need to remember that its domain is R∖{π2+kπ|k∈Z}. Therefore, we see it is the quotient of two functions both of which are differentiable- sin and cos. Hence, it is differentiable.

How do you prove the derivative of tan x?

Ans. So, there are two ways that you can use to find the tan derivative formula. Therefore, you might go for normal differentiation where you will need the quotient rule. On the other hand, you might use the first principle. However, the latter is much more complex but in both cases, you get the same answer- sec^2 x. If you want to see the process in detail, scroll up and check out the “tan derivative proof” section of the article for a better understanding.

What does tan integrate to?

Ans. So, just like you can have a tan derivative, you can have an integral as well. Because you can integrate tangent functions. So, let us say the variable here is x. Therefore, tan x would integrate to give ln Icos xI + c. Moreover, the “c” becomes crucial as it is the integral constant for any indefinite integration that has no limits.