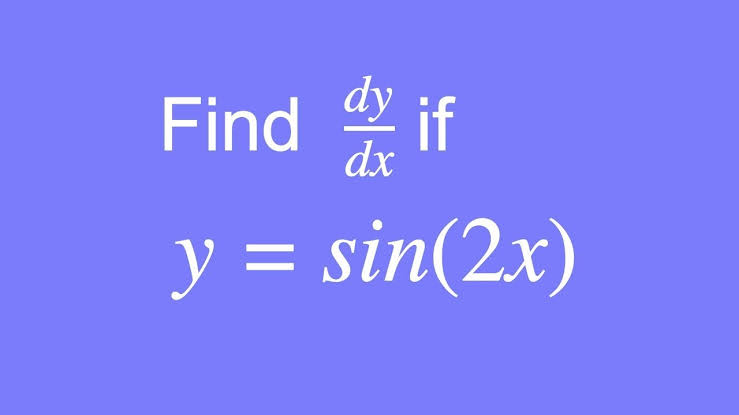Differentiation of trigonometric features is likewise a mathematical approach for acquiring the by-product of a trigonometric characteristic, or its fee of extrade with respect to a variable.  However, not unusual place trigonometric features are sin(x), cos(x), and tan(x) (x). For example, f ′(a) = cos(x) is the by-product of f(x) = sin(x) (a). The fee of extrade of sin(x) at a sure factor is denoted through f ′(a).

However, sin(x) and cos(x) may be used to derive the derivatives of all round trigonometric features. However, to differentiate the consequent expression, observe the quotient rule. Then, using implicit differentiation and the through-merchandise of regular trigonometric features is needed to discover the derivatives of inverse trigonometric features.

Let us assessment some statistics approximately sin 2x earlier than shifting directly to locating the by-product. 2x is a double perspective, and sin 2x = 2 sin x cos x is one of the double perspective formulas. Because sin 2x has a double perspective, its by-product has a double perspective as well. However, with the use of numerous methods, we can display that the by-product of sin 2x is two cos 2x in this article.

Let’s observe some extraordinary approaches to get the by-product of sin 2x and use it to clear up some cases. Also, don’t forget the distinction among sin 2x and sin2x derivatives.

What is the Derivative of Sin2x

2 cos 2x is the by-product of sin2x. However, that is written as d/dx (sin 2x) = 2 cos 2x (or) (sin 2x)’ = 2 cos 2x in math. Then, the sine characteristic with a double perspective is f(x) = sin 2x. However, differentiation of sin 2x may be carried out in a whole lot of approaches, including:

• Using the primary precept
• Then, Using the chain rule
• Then, Using product rule

Derivative Definition

A by-product is the fee of extrade of a characteristic with admire to a variable in mathematics. As a result, derivatives are essential in fixing calculus and differential equation problems. In general, scientists examine converting systems (dynamical systems) to decide the fee of extrade of a variable of interest, then plug that data right into a differential equation and use integration strategies to attain a characteristic that may be used to are expecting how the unique machine will behave below diverse conditions.

Read Also: Interval of convergence calculator- meaning, use, series

A characteristic that isn’t always non-stop can not be differentiable on account that each differentiable characteristic needs to be non-stop. A characteristic may also or might not be differentiable, even though it’s miles non-stop.

Derivative of Sin2x Formula

2 cos 2x is the derivative of sin 2x. It can be represented as d/dx (sin 2x) = 2 cos 2x (sin 2x) = 2 cos 2x (sin 2x)’ = 2 cos 2x

Derivative of Sin2x using first principle

The first principle is used to differentiate sin 2x. Assume that f(x) = sin 2x in this case. Then sin 2(x + h) = sin (2x + 2h) = f(x + h) = f(x + h) = f(x + h) = f(x + h) = f(x + Using the primary precept, replacement those numbers withinside the by-product formula ( the restriction definition of the by-product),

f'(x) = limₕ→₀ [f(x + h) – f(x)] / h

Then, f'(x) = limₕ→₀ [sin (2x + 2h) – sin 2x] / h

Similarly, we can simplify this limit in two methods.

Method 1

By one of the trigonometric formulas, sin C – sin D = 2 cos [(C + D)/2] sin [(C – D)/2]. However, applying this, we get,

f'(x) = limₕ→₀ [2 cos[(2x + 2h + 2x)/2] sin[(2x +2h – 2x)/2] ] / h

Then, f'(x) = limₕ→₀ [2 cos[(4x + 2h)/2] sin (h) ] / h

Then, f'(x) = 2 limₕ→₀ [cos[(4x + 2h)/2] · limₕ→₀ [sin h / h]

However, using limit formulas, lim ₓ→₀ (sin x/x) = 1. So

f'(x) = 2 [cos[(4x + 0)/2] · (1) = 2 cos (4x/2) = 2 cos 2x

Thus, we have proved that the derivative of sin 2x is 2 cos 2x.

Method 2

By sum and difference formulas,

sin (A + B) = sin A cos B + cos A sin B

Using this,

f'(x) = limₕ→₀ [sin 2x cos 2h + cos 2x sin 2h – sin 2x] / h

Then, f'(x) = limₕ→₀ [ – sin 2x (1- cos 2h) + cos 2x sin 2h] / h

Then, f'(x) = limₕ→₀ [ – sin 2x (1 – cos 2h)]/h + limₕ→₀ (cos 2x sin 2h)/h

Similarly, f'(x) = -sin 2x limₕ→₀ (1 – cos 2h)/h + (cos 2x) limₕ→₀ sin 2h/h

However, using double angle formulas, 1 – cos(2h) = 2 sin2(h).

Hence, f'(x) = -sin 2x limₕ→₀ (2 sin2(h))/h + (cos 2x) limₕ→₀ sin 2h/h

= -2sin 2x [limₕ→₀ sin (h) / (h) · limₕ→₀ sin h] + (cos 2x) (limₕ→₀ sin 2h/h)

However, by one of the limit formulas, lim ₓ→₀ (sin x/x) = 1 and lim ₓ→₀ (sin ax/x) = a.

So, f'(x) = -2sin 2x (1 · sin 0) + cos 2x (2)

Then, f'(x) = -2sin 2x(0) + 2 cos 2x (From trigonometric table, sin 0 = 0)

Therefore, f'(x) = 2 cos 2x

As a result, we are able to deduce that the by-product of sin 2x is two cos 2x.

The first precept is used to discover the by-product of sin 2x.

Derivative of Sin2x using product rule

Derivative of Sin 2x Proof Product Rule

To derive the derivative of f(x) = sin 2x using the product rule, we must express sin 2x as the product of two functions. Using the double angle formula of sin, we get Sin 2x = 2 sin x cos x. Consider the equations v = cos x and u = 2 sin x. Then v’ = -sin x and u’ = 2 cos x are calculated. As a general rule,

f ‘(x) = uv’ + vu’

= (2 sin x) (- sin x) + (cos x) (2 cos x)

Equals 2 (cos2x – sin2x)

= 2 cos 2x

This is because, by the double angle formula of cos, cos 2x = cos2x – sin2x.

Thus, we have found the derivative of sin 2x by using the product rule.

n^th Derivative of Sin2x

The derivative of sin 2x created by iteratively differentiating sin 2x for n times is called the nth derivative. Discover the first derivative, the second derivative, and so on until the nth derivative of sin 2x is determined to understand the trend/pattern.

2 cos 2x is the first derivative of sin 2x.

The second derivative of sin 2x then becomes -4 sin 2x.

Then sin 2x’s third derivative is -8 cos 2x.

Similarly, sin 2x’s fourth derivative is 16 sin 2x.

Likewise, the 5th derivative of sin 2x is 32 cos 2x, and vice versa.

Then sin 2x’s 6th derivative is -64 sin 2x.

Similarly, the seventh derivative of sin 2x is -128 cos 2x.

Likewise, the 8th derivative of sin 2x, for example, is 256 sin 2x, and so on.

Using this trend, the nth derivative of sin 2x can be calculated as follows:

(sin 2x)(n) = (sin 2x)(n)(n)

Derivative of Sin2x using chain rule

Derivative of Sin 2x Proof Chain Rule

In this example, we’ll try to apply the Chain Rule to three functions that are nested within each other. This is also the first and most important role. The sin function comes after that, followed by the cos function. Create each one as if it were one-of-a-kind using the Chain Rule (regardless of the argument). As a visual aid, we’ll multiply each individual derivative together as well. To distinguish each derivative, we can use a red-blue-green colour scheme.

The chain rule, on the other hand, is a formula in calculus that computes the derivative of a collection of two or more functions. Only if f and g are both functions is this true. As a result, the derivative of the composite function f g is expressed by the chain rule as the derivation of f and g.

However, if g is differentiable at x and f at g(x), the composite function F = f g defined by F(x) = f(g(x)) is differentiable at x, and F’ is provided by the product F’ (x) = f'(g(x)).g'(x)

If y = f (u) and u = g(x) are both differentiable functions in Leibniz notation, then dy/dx = dy/du.du/dx

The Chain Rule can be written in either prime or non-prime notation (f g)'(x) = f'(g(x))g’ or in compound notation f(g)'(x) = f'(g(x)g'(x)

f‘(x) = 4 sin(2x) cos(2x)

This function can be condensed using a trigonometric identity (giving: 2sin(4x)), but we don’t want to complicate things.

Derivative of Sin2x with respect to x

Sin2 x has a derivative.

The derivative of sin2x is not the same as the derivative of sin 2x. The derivative of sin2x is sin 2x. Let’s see what we can come up with. Assume that f(x) is equal to sin2x. A formula for f(x) = (sin x)2 may be found here. To find its derivative, we can utilize a combination of the power rule and the chain rule. The result is f'(x) = 2(sin x) d/dx(sin x) = 2 sin x cos x = sin 2x (by using the double angle formula of sin)

As a result, the derivative of sin2x is sin 2x.

Important Points to Remember About the Sin 2x Derivative:

The derivative of sin 2x is 2 cos 2x.

The cos axe is usually the derivation of the sin axe.

Sin 2x and sin2x do not have the same derivatives.

d/dx (sin 2x) = 2 cos 2x

d/dx (sin2x) = sin 2x

Derivative of Sin2x cos2x

The value of sin2x Cos 2x is calculated using trigonometric double angle formulas. In the derivation, the values of sin 2x and cos 2x are employed.

From trigonometric double angle formulas, trigonometric double angle formulas are derived.

Sin 2x = 2 sin x cos x ————(i)

And,

Cos 2x = Cos2x − Sin2x

= 2 cos2x − 1 ————(ii) [Since Sin2 x + Cos2 x = 1]

= 1 − 2Sin2x ————(iii)

Now, to get the value of Sin 2x Cos 2x, multiply equation (i) with (ii) or (i)

Consider equation (i) and (ii)

Sin 2x = 2 sin x cos x

And,

Cos 2x = 2 cos2x − 1

Multiply them to get,

Sin 2x Cos 2x = 2 Sin x Cos x (2 cos2x − 1)

= 4 Sin x Cos 3x − 2 Sin x Cos x

= 2 Cos x (2 Sin x Cos2 x − Sin x)

Now, consider equation (i) and (iii),

Sin 2x = 2 sin x cos x

And,

Cos 2x = 1 − 2 Sin2x

Multiply them to get,

Sin 2x Cos 2x = 2 Sin x Cos x (1 − 2 Sin2x)

= 2 Sin x Cos x − 4 Sin3 x Cos x

= 2 Cos x (Sin x – 2 Sin3 x)

So,

Sin 2x Cos 2x = 2 Cos x (2 Sin x Cos2 x − Sin x)

Or,

Sin 2x Cos 2x = 2 Cos x (Sin x – 2 Sin3 x)

Derivative of Sin 2x Cos 2x

d/dx (Sin 2x Cos 2x) = 2Cos(4x)

Proof:

Sin(2x)cos(2x)

= ½(2sin(2x)cos(2x))

Or, ½Sin(4x)

Now, differentiate the given function with respect to x:

d/dx [½ Sin (4x)]

= ½[ d/dx (Sin(4x) ) ]

= ½[Cos (4x) d/dx (4x)]

= ½[Cos (4x) (4)]

So, d/dx (Sin 2x Cos 2x) = 2 Cos(4x)

Derivative of Sin2x with respect to eCos x

Derivative of sin²x with respect to ecos x

Differentiate, y = sin²x with respect to x,

dy/dx = d(sin²x)/dx

= 2 sin x × cos x

Hence, differentiation of sin²x with respect to x is dy/dx = 2sinx.cosx

Now differentiate z = e^cos x with respect to x,

dz/dx = d(ecos x)/dx

= ecos x × d(cos x)/dx

= ecos x × (-sinx)

= -sinx . ecos x

As a result, dz/dx = -sinx is the differentiation of e cos x with respect to x.

We derive differentiation of sin2x with regard to e cos x by dividing (dy/dx) by (dz/dx).

As a result, (dy/dx) / (dz/dx) = (2 sinx.cosx) / (-sinx.cos x), or dy/dz = -2 cos x/e cos x.

Derivative of Sin2x /1+cosx

Derivative of sin2x/ (1 + cosx)

Let y = sin2x/(1 + cosx)

Thus using quotient rule ,

dy/dx = {(1 + cosx) × d/dx (sin2x) – sin2x × d/dx (1+cosx)} / (1+cosx)2

Therefore, dy/dx = {(1+cosx) * sinx.cosx – sin2x(-sinx)} / (1+cosx)2

Then, dy/dx = {sin2x + sinx.cosx + sin3x} / (1+cosx)2

Derivative of Sin2x Cos3x

Derivative of sin2x cos3x

In this question,

ddx (sin2x cos3x) = (sin2x) × d/dx (cos3x)+(cos3x) × d/dx (sin2x)

Thus, d/ dx (sin 2x.cos 3x) = (sin 2x) × d/dx (cos 3x)+(cos 3x) × d/dx (sin 2x)

Then, d/ dx (sin 2x.cos 3x) = (sin 2x) × (−sin 3x) × 3+(cos 3x) × (cos 2x) × 2

= (sin 2x) × (-sin 3x) × 3+(cos 3x) × (cos 2x) × 2

[We are using chain rule]

= (−3 sin 2x sin3x + 2 cos3x cos2x)

Therefore, d/ dx (sin 2x.cos 3x) = (-3 sin 2x sin 3x + 2 cos 3x cos 2x)

Derivative of Sin2x wrt Cos2x

Sin2x derivative with regard to cos2x

We already know that sin 2x equals 2sinxcosx and (uv)’=u’v+v’u. This is referred to as the product differentiation rule.

d/dx (sin2x) = d/dx(2 sinx cosx) = 2 d/dx (sinx cosx) is the result.

d/dx sin2x = 2sinx.d/dx cosx + 2cosx.d/dx sinx is the product rule of differentiation.

We now know that sin’s derivative is cos, and that cos x’s derivative is -sin x.

Hence we have,

d/dx sin 2x = 2 sin x (−sinx) + 2 cos x × cos x = 2(cos 2x − sin 2x)

We know that cos 2x = cos2x − sin2x

Hence, we have

d/dx sin2x= 2(cos 2x)= 2 cos2x

Derivative of Sin2x + cos2x

From the given

y=sin²x+cos²x

The right side of the equation is =1

y=1

dy/dx=d/dx(1)=0

or we can do it this way.

y = sin² x + cos² z

Then, dy/dx = 2 × (sin z)^ (2-1) × d/dx ( sin x ) + 2(cos x)^ (2-1) × d/dz ( cos z )

Likewise, dy/dx= 2 × sin x × cos z + 2 cos z (- sinz)

Then, dy/dx = 2 × sin z × cos z –  2 × sin z × cos z

Then, dy/dx = 0

Derivative of ln sin2x

Take advantage of the chain rule.

Your function can be decomposed into logarithm, square, and sinus components as follows:

f(u)=ln(u)

u(v)=v²(x)

v(x)=sin(x)

The three derivatives of those three functions must now be computed (and the appropriate u and v values must be entered):

f‘(u)=1/u=1/v²=1/sin²x

u‘(v)=2v=2sinx

v‘(x)=cos(x)

All that’s left to do now is multiply those three derivatives:

f'(x) = f'(u) × u'(v) × v'(x) = 1/ sin² x 2 sin x cos x

= ( 2 cos x ) / sin x

Derivative of Sin2x at x=π/2

sin 2x at x = π/2 Given: f (x) = sin 2x By using the derivative formula,

f(a) = limₕ→₀ [ { f (a+h) – f (a) } / h] where h is a positive integer of a small size.

Derivative of sin2x at x = π/2 is given as,

f’ ( π/2 ) = limₕ→₀ [ { f ( π/2 + h ) – f (π/2) } / h ]

=limₕ→₀ [ sin { 2 × ( π/2 + h )} – sin2 × π/2 ] / h

=limₕ→₀ {sin ( π + 2h ) – sin π}/ h. [Hence, sin (π+x) = – sinx and sin π = 0]

=limₕ→₀ (-sin 2h – 0)/ h

=limₕ→₀ sin 2h / h

[Because it is of an ambiguous nature. To determine the limit, we’ll use the sandwich theorem.]

By multiplying the numerator and denominator by two, we arrive at

= – limₕ→₀ (sin 2h / 2h ) × 2 = – 2 limₕ→₀ ( sin 2h / 2h)

By using the formula lim x→₀ sinx / x = 1, we get

f’ ( π/2 ) = – 2 × 1 = -2

Therefore, the derivative of sin 2x at x = π/2 is (-2).

Find dy/dx if y = sin2x

To solve this, you’d apply the chain rule. To do so, you’ll need to figure out what the “outer” function is, as well as the “inner” function that’s part of the outer function.

In this situation, sin(x) is an inner function that is part of the sin2 function (x).

As a result, the chain rule is as follows:

F'(x)=f'(g(x))(g'(x)) where g(x) is an inner function and f(g(x)) is an outer one.

1. The derivative of the outer function(with the inside function left alone) is:

f'((sin(x))^2) = 2sin(x)

1. The derivative of the inner function:

g'(sin(x)) =cos(x)

• Combining the two steps through multiplication to get the derivative as :

2sin(x)cos(x).

Frequently Asked Questions about Derivative of Sin2x

What is the derivative of sin^2x?

d/dx of sin^2 x

We’ll apply the chain rule in this case.

However, to begin, separate the square half, which equals 2, to get the solution. 2sinx

Then, to get the answer, differentiate the trigonometric function using sin x as an example. cos x

Then, take the x, which is one, and divide it.

And multiply them all by 2sinx* cosx * 1 =2sin x cos x, which can alternatively be represented as sin 2x, according to the chain rule.

Therefore, d/dx of sin^2 x= 2sin x cos x= sin2x

What is the derivative of sin2x?

In particular, dy/dx= 2*cos (2x). Remember the chain rule: distinguish the outside function first, then differentiate the internal function. The derivative of sin(x) with respect to x is cos(x), whereas the derivative of 2x with respect to x is only 2.

Is sin2x the same as 2sinx?

2 is the sine of 2 multiplied by x, or twice the angle x, whereas 1 is multiplied by. As a result, we’ve also got two very different outcomes. Because sine is a periodic (repeating) waveform, these graphs will cross at regular intervals, giving the same answer for both equations!

What is the formula of sin2x?

2. Double-angle formulas: sin 2x = 2sin x cos x, cos 2x = cos2x − sin2x = 2cos2x − 1=1 − 2sin2x.

What does Derivative Of sin^2x mean?

Tech Mechanical Engineering, Institute of Engineering and Management. Meanwhile, on May 13th, 2017, I received a response to my query. Because it is the “sine of (x-squared),” Sin x2 is an ordinary sine function. The sine function is not the same as Sin2x, which stands for “sine-squared of x.”

How do you integrate Cos 2x?

To put cos2 x together, follow these steps:

• Using the half-angle identity for cosine, rewrite the integral in terms of cos 2x.
• Then, use the Constant Multiple Rule to move the denominator outside the integral.
• Then, using the Sum Rule, distribute the function and divide it into several integrals.
• Finally, calculate the two integrals separately.

How do you integrate sin^2(x)?

Sin2x cannot be directly integrated (x). Then, to answer the problem, use trigonometric identities and calculus substitution procedures. However, substitute 1/2 times the integral of (1 – cos(2x)) dx into the integral using the half-angle formula sin2(x) = 1/2*(1 – cos(2x)).

What is the chain rule in calculus?

The derivative of f(g(x)) is f'(g(x))g’, according to the chain rule (x). To put it another way, it aids in the differentiation of *composite functions*. Sin(x2), for example, is a composite function since it can be written as f(g(x)) for f(x)=sin(x) and g(x)=x².

What is the Derivative Of sin^2x?

Tech Mechanical Engineering, Institute of Engineering and Management. Meanwhile, on May 13th, 2017, I received a response to my query. Because it is the “sine of (x-squared),” Sin x2 is an ordinary sine function. The sine function is not the same as Sin2x, which stands for “sine-squared of x.”

What does Cos 2x mean?

The Cos(2x) trig function is a “double angle” trig function. There’s nothing to “do” on a calculator unless we’re trying to calculate the cosine for a value of 2x. In this case, x is an angle and 2x is twice the measure of that angle.

Is the derivative of sin2x sin²x?

The derivative of sin 2x is 2 cos 2x. However, we write this mathematically as d/dx (sin 2x) = 2 cos 2x (or) (sin 2x)’ = 2 cos 2x. Likewise, here, f(x) = sin 2x is the sine function with a double angle.

What are the double angle formulas?

The sum formulas, where α=β, are a specific case of the double-angle formulas. However, the sum formula is used to get the double-angle sine formula. sin(α+β)=sinαcosβ+cosαsinβ. sin(θ+θ)=sinθ cosθ+cos θ sin θ sin(2θ)=2sinθcosθ.

What does sin 2x equal?

Hence, the formula of sin square x using Pythagorean identity is sin^2x = 1 – cos^2x. This formula of sin^2x is used to simplify trigonometric expressions.