In mathematics, many objects can be neighboring, such as adjacent forms, line segments, angles, sides, and so on. The term neighboring in geometry, as in general usage, refers to nearby (side-by-side) parts in form. Usually used to describe lines, arcs, or angles. The neighboring side of a right triangle is the side that follows the angle in trigonometry.
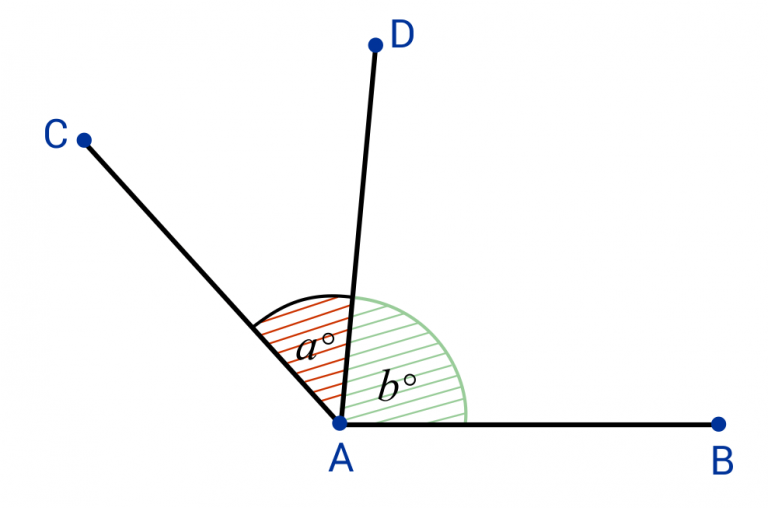
In mathematics, adjacent can refer to a variety of things. Although we used it to refer to line segments and angles. Adjacent angles are any two angles that share a shared ray or side, a common vertex, and whose interiors do not overlap. In this article, we are talking about these angles. So, keep reading to know more about it.
Adjacent Angles meaning
Adjacent angles are those with a shared arm (side) and a common vertex but do not overlap. When two rays intersect at the same endpoint, an angle is generated, and neighboring angles are those that are always put next to each other.
The definition of adjacent is “nearby” or “next to.” Two nearby dwellings are an example of adjacent. People on our block, we considered them our neighbors. So, who is our next-door neighbor? A person who lives in the same house or flat as us. Adjacent can mean two things: touching or sharing the same wall or border. What about two lines those intersect at a polygon’s vertex? Can they be thought of as neighboring sides? The two sides that meet at the vertex of a triangle or other polygon are neighboring.
Adjacent angles examples
Linear pair
Imagine a cross to get a sense of what a linear pair looks like. Four angles are formed when two lines intersect.
If you look at the image on the right, you will notice four angles labeled 1, 2, 3, and 4. The linear angles in this picture are 1 and 3, 3 and 2, 2 and 4, 4 and 1.
If two angles sum up to 180 degrees, you may triple-check that they are a linear pair. Because all linear pairs of angles are supplementary, they always add up to 180 degrees. If the angles are contiguous and sum up to 180 degrees, you may be certain that they are a pair of angles.
Vertically opposite angles
Vertically opposite angles are not exactly neighboring angles, but if there are adjacent angles, there are likely to be some vertically opposite angles as well.
Vertical angles have already been investigated, however to clarify, vertical angles share the same vertex but no sides. In the example above, the angles 3 and 4 and 1 and 2 are regarded vertically opposed.
One distinguishing feature of vertically opposite angles is that they have the same measurement. For example, if angle 1 is 30 degrees, angle 2 is likewise 30 degrees.
Examples
Example 1: State whether or not the characteristics of neighboring angles are true or untrue.
a.) Adjacent angles are always additive.
b.) Adjacent angles always have the same vertex and arm.
Solution:
- False, neighboring angles are not always supplementary. Any two of these angles that create a straight line form extra adjacent angles.
- True, neighboring angles always have a shared vertex and an arm in common.
Example 2: Determine the value of x.
If m∠AOB = 110°, m∠AOC = x and m∠ COB = 70°
Solution:
From figure:
m∠AOB = 110°
Then, m∠AOC = x
m∠ COB = 70°
Now, from figure: ∠AOB = ∠AOC + ∠COB
m∠AOB = m∠AOC + m∠COB
110° = x + 70°
x = 110° – 70°
x = 30°
Example 3: In the given figure, is ∠1 adjacent to ∠2?
Solution:
In the diagram, ∠1 does not share the vertex of ∠2.
Because it does not follow the crucial characteristic of neighboring angles,
∠1 and ∠2 are not neighboring.
Adjacent angles of a parallelogram are
A parallelogram’s adjacent angles are supplementary.
Justification
Consider the Parallelogram ABCD.
To demonstrate: A + B Equals 180 degrees, C + D = 180 degrees
AB ∥ CD and AD are transversals.
Interior angles on the same side of a transversal are said to be supplementary.
As a result, A + D = 180°.
Likewise, B + C = 180°, C + D = 180°, and A + B = 180°.
As a result, the sum of any two adjacent parallelogram angles equals 180°.
As a result, it is demonstrated that any two adjacent or successive parallelogram angles are supplementary.
Adjacent angles of a quadrilateral
A quadrilateral, a basic closed shape made by combining four line segments. Four sides, four angles, four vertices, and two diagonals made it.
On a quadrilateral, A, B, C, and D are four points in a plane where none of them are collinear and the line segments AB, BC, CD, and DA do not overlap except at their end points.
The figure created by these four line segments created the figure. These segments are the quadrilateral ABCD.
In an ABCD quadrilateral:
- Its vertices are the four points A, B, C, and D.
- Its sides are the four line segments AB, BC, CD, and DA.
- Then, its angles are ∠DAB, ∠ABC, ∠BCD, and ∠CDA. So, A, B, C, and D indicated these, respectively, and
- Its diagonals are the line segments AC and BD.
A quadrilateral’s neighboring angles are two angles that share a common arm.
(∠A, ∠B), (∠B, ∠C), (∠C, ∠D), and (∠D, ∠A) are four pairs of neighboring quadrilateral ABCD angles seen in the illustration.
Adjacent angles of a rhombus
A rhombus is a subset of a parallelogram. The opposing sides of a rhombus are parallel, and the opposite angles are equal. Furthermore, all of the sides of a rhombus are the same length, and the diagonals intersect at right angles. We referred a rhombus as a diamond or rhombus diamond. Rhombi or rhombuses are the plural form of rhombus.
The following are some interesting rhombus angle facts:
- First, the inner angles of a rhombus are four.
- Then, the total of a rhombus’ internal angles equals 360 degrees.
- Then, a rhombus’s opposite angles are equal to each other.
- Also, the adjacent angles are extraneous.
- Then, Diagonals in a rhombus intersect at right angles.
- Then, these angles are bisected by the diagonals of a rhombus.
Example 1
A rhombus’s two diagonal lengths, d1 and d2, are 6cm and 12cm, respectively. Determine its location.
Solution:
d1 = 6cm diagonal
12 cm diagonal d2
A = (d1 x d2)/2 square units of rhombus area
Then, (6 x 12)/2 = A
Then, 72/2 = A
At last, 36 cm2 = A
As a result, the rhombus area is 36 cm2.
Example 2
Find the diagonal of a rhombus whose size is 121 cm2 and greatest diagonal length is 22 cm.
Solution:
Given: rhombus area = 121 cm2, and d1 = 22 cm.
We derive A = (d1 x d2)/2 square units using the Area of the Rhombus formula.
(22 x d2)/2 = 121
11 x d2 = 121
or 11 = d2
As a result, another diagonal length is 11 cm.
Example 3
What are the fundamental features of a rhombus?
Solution:
The rhombus has the following fundamental properties:
- The two angles are equivalent.
- The diagonals meet at a 90-degree angle.
- The diagonals cut the opposing internal angles in half.
- The adjacent angles are extraneous.
Example 4
What is the circumference of a rhombus with six equal sides?
Solution:
Given that the side of the rhombus = 6cm
Because all of the sides are equal,
4 x side = perimeter
4 x 6 = P
24cm = P
Adjacent angles of trapezium
A trapezium, often known as a trapezoid, is a quadrilateral having two parallel sides. Because it has two parallel sides, a parallelogram is also known as a trapezoid. The base of the trapezoid is the pair of parallel sides, whereas the legs of the trapezoid are the non-parallel sides. The mid-segment is the line segment that links the midpoints of the legs of a trapezoid.
Every trapezium has the following characteristics:
Angle: 360° is the sum of the angles of a trapezoid-like other quadrilateral. As a result, in a trapezoid ABCD, ∠A+∠B+∠C+∠D = 360°.
Two angles on the same side are supplementary, which means that the total of two neighboring angles equals 180°.
Its diagonals cross each other.
The mid-length segment is equal to half the total of the bases. In the diagram above, the mid-segment equals 1/2 (AB+CD).
Legs of the trapezium are congruent in exceptional situations of the isosceles trapezium. This indicates that, although being non-parallel, the length of both legs is the same.
Adjacent angles of a parallelogram are supplementary
The parallelogram’s neighboring angles are also known as the adjacent parallelogram’s angles that are adjacent to each other. A parallelogram has four pairs of neighboring angles that are supplementary.
A parallelogram’s neighboring angles are those that are arranged next to each other in sequence. Look at the parallelogram below to observe the four pairs of neighboring angles. These angles are also known as parallelogram consecutive angles. Each adjacent angle here adds up to 180°. The parallelogram has four pairs of neighboring angles: ∠P and ∠Q, ∠Q and ∠R, ∠R and ∠S, and ∠S and ∠P.
The qualities of a parallelogram’s neighboring angles are as follows:
- A parallelogram’s neighboring angles are supplementary.
- A parallelogram has four pairs of neighboring angles.
- If the neighboring angles of a parallelogram are equal, the parallelogram is a rectangle; if the sides are equal, the parallelogram is a square.
- A Parallelogram’s Adjacent Angles Are Supplementary
- A parallelogram’s two neighboring angles are always supplementary. This indicates that the sum of these successive angles is 180°.
Let us examine this fact using the following evidence. Consider the following diagram in relation to the proof presented below.
Proof
If ABCD is a parallelogram, the opposing sides must be parallel.
- Consider AB || DC, where AD and BC are the transversals.
- When a transversal cuts two parallel lines, the co-interior angles on the same side of the transverse are additional. In this situation, ∠A + ∠D equal 180°, and ∠B + ∠C equals 180°.
- If we accept AD || BC, then AB and DC are transversals. Because the co-interior angles of two parallel lines are supplementary, ∠A + ∠B = 180° and ∠D + ∠C = 180° in this situation.
- As a result, the product of any of these angles is supplementary. This indicates that ∠A + ∠B equals 180°, ∠B + ∠C equals 180°, ∠C + ∠D equals 180°, and ∠D + ∠A equals 180°.
Example 1
A parallelogram’s two neighboring angles are (3x – 4) and (3x + 16). Determine the value of x and the length of each angle.
The value of x may be found using the following procedures if the neighboring angles of a parallelogram are (3x – 4) and (3x + 16).

Step 1: Because parallelogram neighboring angles are supplementary, we may express it as (3x – 4) + (3x + 16) = 180.
Step 2: When we solve this, we obtain 6x + 12 = 180. As a result, x = 28.
Step 3: By changing the value of x to 28 in (3x – 4), we obtain (3 28) – 4 = 84 – 4 = 80°.
Step 4: Similarly, the other angle’s value may be computed by putting x = 28 in (3x + 16). This translates to 3x + 16 = (3 28) + 16 = 100°. As a result, the two nearby angles are 80° and 100°. It is possible to demonstrate that they add up to 180°, i.e., 80 + 100 = 180°.
Example 2
If two neighboring parallelogram angles are (5x – 5) and (10x + 35). Determine the value of x and the angle ratio.
Solution: If two neighboring parallelogram angles are (5x – 5) and (10x + 35), let us first determine the value of x using the techniques below:
Step 1: Because neighboring angles of a parallelogram are supplementary, we may write this as (5x – 5) and (10x + 35) = 180.
Step 2: When we solve this, we obtain 15x + 30 = 180. This results in the number x = 10.
Step 3: Substituting the value of x = 10 in (5x – 5) yields (5 10) – 5 = 50 – 5 = 45°.
Step 4: Similarly, the other angle’s value may be computed by inserting x = 10 in (10x + 35). This indicates that 10x + 35 = (10) + 35 = 135°. As a result, these two nearby angles are 45° and 135°, and they add up to 180°, that is, 45 + 135 = 180°.
45/135 = 1:3 is the ratio of the two angles.
Adjacent angles identify
Two key characteristics easily distinguish Adjacent angles. They always have a shared side and a common vertex. Also, if two angles fulfill just one of these criteria, they are not adjacent. Then, it is important for the angles to satisfy both characteristics. Then, for example, if two angles have the same vertex but an angle separates them, this indicates that they do not share a common side. So, as a result, they cannot be adjacent angles.
Adjacent angles in rectangle
A rectangle’s angles are all right angles. A rectangle is a two-dimensional closed shape with four sides and four corners. It is defined by two dimensions: length and breadth. The length of the rectangle is known as its length, while the width is known as its width.
A rectangle is a two-dimensional shape that consists of four sides, four vertices, and four angles. Because a rectangle is a quadrilateral with four equal angles, the neighboring sides of a rectangle meet at the correct angle. As a result, the angle created by its opposite sides is 90°. A rectangle’s four sides are not equal, but its four angles are.
Let us summarize the characteristics of angles in a rectangle as shown in the diagram above:
- Each of the four internal angles is a right angle.
- The sum of a rectangle’s internal angles equals 360°.
- A rectangle’s neighboring angles are all the same size.
- Any two successive rectangle angles are supplementary.
- A rectangle’s diagonals intersect but do not create right angles in the middle.
Rectangular Angle Sum
We know that a rectangle is merely a quadrilateral, and the sum of all its internal angles is 360° according to the angle sum feature of quadrilaterals. We also know that the four angles of a square are equivalent, one at each vertex. Thus, at each vertex, the interior angle of a rectangle equals 360°/4 = 90°. A rectangle’s inner angle at each vertex is 90°.
Rectangle Diagonal Angles
A rectangle’s diagonals are equal in length and bisect each other. The diagonals cross but do not create right angles in the middle. As at each diagonal, they produce linear pairs of angles, obtuse angle + acute angle. Because rectangle diagonals do not bisect the corresponding vertex angles into equal angles, the rectangle is considered a square if its diagonals bisect each other at right angles.
A diagonal divides a rectangle into two congruent triangles, namely right triangles with the same hypotenuse. Each diagonal serves as the hypotenuse for the resulting right triangles. Using Pythagoras’ theorem, d2 = l2 + w2, where d is the diagonal, l is the length, and w is the width of the rectangle. √(d2) = √( l2 + w2) after taking the square root on both sides. As a result, the formula for a rectangle’s diagonal is: √(a² + b²).
Example 1
ABCD is a square. Determine the angle x.
Rectangle Angles: Determine x
Solution:
Rectangle ABCD is provided.
Because triangle ABC is a right triangle, its three angles add up to 180°.
180° = 90° + (2x+20) ° + (3x) ° (Angle sum property)
180 – 90 = 2x + 3x + 20
5x = 90 – 20
x = 70/5 = 14 degrees
As a result, (2x+20)° = 2 14 + 20 = 28 + 20 = 48°
(3x°) = 3 14 = 42°
As a result, the two angles provided as (2x+20)° and (3x)° are 48° and 42°, respectively.
Example 2
Find the diagonal of a rectangle with dimensions of 6 and 4 units using the properties of angles of the rectangle.
Solution:
The dimensions of a rectangle are given as 6 and 4 units.
The diagonal of a rectangle = (d) = (l2 + w2) according to the characteristics of angles of the rectangle
Rectangle diagonal length = (6)2+(4)2 = 52 = 7.21 units
As a result, the diagonal length of the rectangle with dimensions of 6 and 4 units is 7.21 units.
Adjacent angles and vertical angles
Identifying the difference between neighboring and vertical angles is a crucial ability in geometry. To comprehend the difference between these two sorts of angles, consider two straight lines meeting to form a cross.
Read Also: Remainder Theorem, Definition, Formula and Examples
Four angles are generated when a cross is made. We can recognize neighboring angles because they have a shared side and a common vertex. But how can we know what a vertical angle is? Finding a vertical angle is as simple as finding an adjacent angle. A group of vertical angles, like neighboring angles, will have a vertex point in common. They do not, however, have to have a common side.
When considering a cross, the vertical angles are those that are opposing each other. This is why they are also known as vertically opposite angles.
Some frequently asked questions
Are adjacent angles 180?
The sum of supplementary neighboring angles is always 180. This is due to the fact that the two angles are adjacent on a straight line, and all angles on a straight line add up to 180. If the neighboring angles are not linear pairs and there is another angle in the mix, the two adjacent angles will not add up to 180.
What are adjacent angles examples?
Adjacent angles are two angles that share a vertex and a side but do not intersect. Angles ∠1 and ∠2 in the diagram are adjacent. They have the same vertex and shared side.
How do you identify adjacent angles?
So, two key characteristics easily distinguish Adjacent angles. They always have a shared side and a common vertex. Also, if two angles fulfill just one of these criteria, they are not adjacent. Then, it is important for the angles to satisfy both characteristics. Then, for example, if two angles have the same vertex but an angle separates them, this indicates that they do not share a common side. So, as a result, they cannot be these angles.
Are these angles supplementary?
The neighboring angles will share the same side and vertex. If the total of two angles is 180 degrees, they are said to be supplementary angles. A linear pair is formed when two additional angles are next to each other.
Which are corresponding angles?
Corresponding angles are generated in geometry when a line known as an intersecting transversal crosses through two straight lines. Corresponding angles are angles obtained in the same relative location at distinct intersections.
What is a pair angle?
When two lines share a similar terminus, known as a vertex, an angle is produced between them, which is known as a pair of angles.
How do you find opposite and adjacent?
It is also the triangle’s longest side. Adjacent and opposing sides are measured in relation to the angle requested and might change appropriately. The opposing side is the side that is opposed to the requested angle, and the adjacent side is the side that is right by the requested angle.
What is adjacent over opposite?
The cosine is the ratio of the neighboring side of a right triangle to the hypotenuse. The sign cos denoted it. cos = a / h. Finally, the tangent is the ratio of the opposing side to the adjacent side. The symbol tan denoted it. tan = o / a.
Are adjacent angles always equal?
Vertical angles are always congruent, meaning they are equal. Adjacent angles are those that emerge from the same vertex. A shared ray connects adjacent angles and does not overlap.
What is adjacent and complementary?
Vertical angles are opposite angles at the intersection of two straight lines, and adjacent angles are two angles that are next to each other. Complementary angles are two angles that add up to 90 degrees, supplementary angles are two angles that add up to 180 degrees, and these angles are two angles that are next to each other.